Un mapa de
Karnaugh (también conocido como tabla de Karnaugh o diagrama de Veitch) es un
diagrama utilizado para la simplificación de funciones algebraicas en forma
canónica. A partir de la tabla de Karnaugh se puede obtener una forma canónica
mínima (con el mínimo número de términos). En este texto emplearemos
indistintamente los términos “mapa” y “tabla” de Karnaugh.
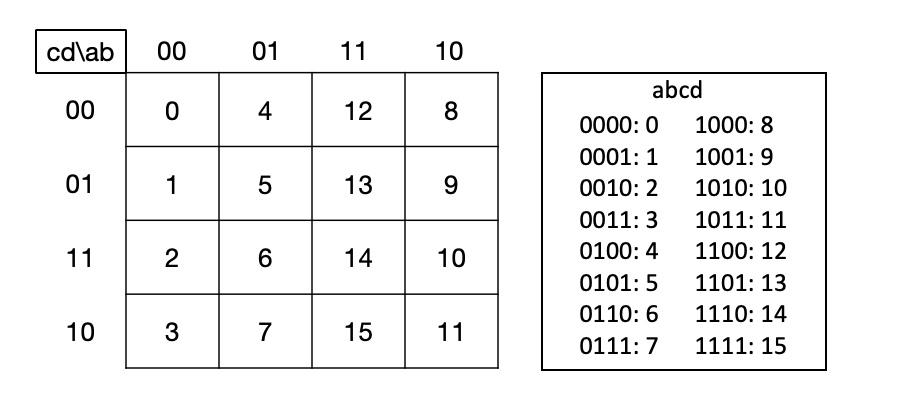
La tabla
de Karnaugh consiste en una representación bidimensional de la función que se
quiere simplificar. Si la función viene expresada como una tabla de verdad,
entonces la tabla de Karnaugh puede verse como una forma alternativa de
representación 2D. Puesto que la tabla de verdad de una función de n variables
posee 2n filas, la tabla de Karnaugh correspondiente debe poseer también 2n celdas.
La construcción de la tabla de Karnaugh pasa por codificar cada celda en código
binario reflejado (o código Gray) de manera que celdas adyacentes tengan un
código que difiere en un solo dígito.
GRAFOS DIRIGIDOS
REPRESENTADOS COMO MATRIZ DE ADYACENCIA
En esta
representación se requiere de una matriz cuadrada ADYA [][] de tamaño N*N,
siendo N el número de vértices del grafo. Esta matriz se llena de la siguiente
manera.
ADYA [ i ][
j ] = 1 Si el vértice i es adyacente al
vértice j.
ADYA[ i ][
j ] = 0 Si el vértice i no es adyacente al vértice j.
Tomemos
como ejemplo el siguiente grafo dirigido. En este
caso la matriz Mat [][] necesaria para
representar el grafo es de tamaño 5*5 y como el
grafo es dirigido, cada lado se representa < i, j >, indicando que el
lado inicia en el vértice i y termina en el vértice j. Como el
grafo es dirigido, debemos determinar de qué manera vamos a representar el
grafo, si entrando o saliendo para nuestro
ejemplo vamos a representar el grafo saliendo.
|
